Question

Assume that when adults with smartphones are randomly selected, 53% use them in meetings or classes. If 30 adult smartphone users are randomly selected, find the

probability that exactly 23 of them use their smartphones in meetings or classes.
The probability is
(Round to four decimal places as needed.)

Answer 1

P(23 ,30 , 0.53 ) = 0.0047

Explanation:

Binomial Distribution

The Binomial Distribution is used to find the probability of an situation where n independent events each with a probability of success equal to p are computed k successes.

The Probability Mass Function is

`P(k,n,p)=\binom{n}{k}p^kq^(n-k)`

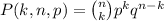
Where
`q = 1-p`

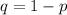
We know 53% of adults with smartphones use them in meetings or classes. This is the probability of success of a single event, or p=0.53. Since q=1-p, q=0.47. We'll compute the probability that exactly 23 out of 30 adults use their smartphones in meetings or classes. Thus n=30, k=23

`P(23,30,0.53)=\binom{30}{23}0.53^(23)0.47^(7)`

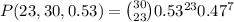
The required probability is

P(23,30,0.53)=0.0047