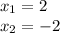Question

Let () = 2x^2 + 1 and () = x^2 + 5. Find the solution to the equation () = () by sketching the functions.

Answer 1

`x_(1)=2\\x_(2)=-2`

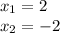
Explanation:

The given expressions are

`()=2x^(2) +1\\()=x^(2) +5`

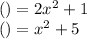
To find
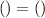`()=()`, we just need to replace each expression and create an equation

`2x^(2) +1=x^(2) +5`

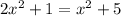
Now, let's solve for
`x`

`2x^(2) -x^(2) =5-1\\x^(2) =4\\x=√(4)`

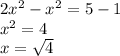
Rememeber that a square root always has to solutions, one positive and one negative.

Therefore, the solutions of the equation is

`x_(1)=2\\x_(2)=-2`

Answer 2

x = -2 or x = 2

Explanation:

A graph is attached. The functions intersect where x = ±2.