Answer:
If this sequence is part of an arithmetic sequence, then its 128-th term would be 256.
Explanation:
The two neighboring terms differ by a constant, 2. As a result, this sequence is likely an arithmetic sequence.
- The first term
 is equal to 2.
is equal to 2. - The common difference
 (second term - first term) is equal to 2.
(second term - first term) is equal to 2.
The formula for the general
 -th term of an arithmetic sequence with first term
-th term of an arithmetic sequence with first term
 and common difference
and common difference
 is:
is:
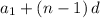 .
.
In this case, that's equal to
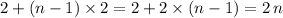 .
.
Let that expression be equal to
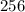 . Solve for
. Solve for
 :
:
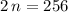
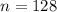 (after dividing both sides by
(after dividing both sides by
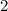 .)
.)
Hence, if this sequence is part of an arithmetic sequence, then the 128-th term would be 256.