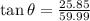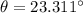Question

A train at a constant 55.0 km/h moves east for 33.0 min, then in a direction 49.0° east of due north for 28.0 min, and then west for 43.0 min. What are the (a) magnitude and (b) angle (relative to east) of its average velocity during this trip?

Answer 1

Step-by-step explanation:

Given

Velocity of train
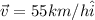`\vec{v}=55 km/h\hat{i}` for
`33 min`

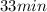
Position vector after
`33 min`

`\vec{r_1}=55* (33)/(60)\hat{i}`

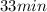
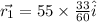
After that it moves
`49^(\circ)` east of due north

Position vector after 43 min

`\vec{r_(21)}=55* (43)/(60)(\cos (49)\hat{j}+\sin (49)\hat{i})`

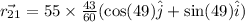
Position of Vector
`\vec{r_2}=55* (43)/(60)(\cos (49)\hat{j}+\sin (49)\hat{i})+55* (33)/(60)\hat{i}`

`\vec{r_2}=(30.25+29.747)\hat{i}+(25.85)\hat{j}`

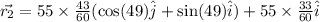
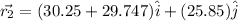
magnitude of final Position
`|r_2|=√(59.99^2+25.85^2)`

`|r_2|=65.32 km`

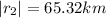
average velocity
`v_(avg)=(displacement)/(time)`

`v_(avg)=(65.32)/(28+43)=(65.32)/(71)`

`v_(avg)=0.92 km/h`

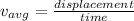
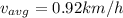
Direction of average velocity will be similar to displacement

`\tan \theta =(25.85)/(59.99)`

`\theta =23.311^(\circ)`