Answer:
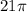 cubic meters per hour
cubic meters per hour
Explanation:
We know that the surface area of a sphere is,
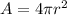 ...........(1),
...........(1),
Where,
r = radius of the sphere,
We have, A =
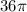 square meters,
square meters,
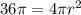
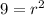
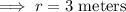
Now, differentiating equation (1) with respect to t ( time ),
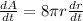
We have,
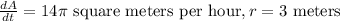
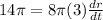
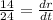
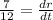
Also, the volume of a sphere is,
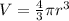
Differentiating with respect to t(time)
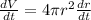
By substituting the values,
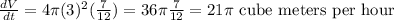
Hence, the rate of change of the volume of the sphere at that instant would be
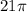 cubic meters per hour
cubic meters per hour