Question

If three prime numbers are randomly selected from the prime numbers less than 30 and no prime number can be chosen more than once, What is the probability that sum of the three prime numbers selected will be even?A) 10%B) 27%C) 30%D) 36.5%E) 42%

Answer 1

C)30%

Explanation:

Prime numbers less than 30 are given below

2,3,5,7,11,13,17,19,23,29

We have to find the probability that sum of three prime numbers selected will be even.

We know that

Sum of any three prime number except 2 will be odd.

Total prime numbers except 2=9

Total prime numbers=10

Probability:P(E)=
`(favorable\;cases)/(total\;number\;of\;cases)`

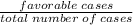
Probability of getting sum of three prime numbers selected will be odd=
`(9C_3)/(10C_3)`

`nC_r=(n!)/(r!(n-r)!)`

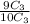
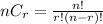
By using formula

Probability of getting sum of three prime numbers selected will be odd=P(E)=
`((9!)/(3!6!))/((10!)/(3!7!))=(9!)/(3!6!)* (3!* 7* 6!)/(10* 9!)`

Probability of getting sum of three prime numbers selected will be odd=P(E)=
`0.7`

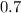
Probability of getting sum of three prime numbers selected will be even=P(E')=1-0.7=0.3=
`0.3* 100=30`%

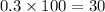By using formula P(E')=1-P(E)