Question

A new medical test has been designed to detect the presence of the mysterious Brainlesserian disease. Among those who have the disease, the probability that the disease will be detected by the new test is 0.7. However, the probability that the test will erroneously indicate the presence of the disease in those who do not actually have it is 0.04. It is estimated that 19 % of the population who take this test have the disease.

If the test administered to an individual is positive, what is the probability that the person actually has the disease?

30. Factories A, B and C produce computers. Factory A produces 2 times as many computers as factory C, and factory B produces 7 times as many computers as factory C. The probability that a computer produced by factory A is defective is 0.032, the probability that a computer produced by factory B is defective is 0.034, and the probability that a computer produced by factory C is defective is 0.056.
A computer is selected at random and it is found to be defective. What is the probability it came from factory C?

32. What is the probability that a 7-digit phone number contains at least one 7? (Repetition of numbers and lead zero are allowed).

Answer 1

Explanation:

The persons who have diseases = 19%

The persons who do not have diseases = 81%

Probability for the test showing positive = Prob of actual disease and shows positive + Prob of no disease but test shows wrong

=
`0.7*0.19+0.04*0.81\\=0.133+0.0324\\=0.1654`

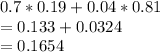
Prob that the person actually has the disease given that the test administered to an individual is positive=
`(0.133)/(0.1654) \\=0.0804`

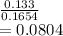
30) A B C total

2x 7x x 10x

P(A) = 0.2, P(B) = 0.7, P(C) = 0.1

Let D be the event that the product is defective

P(D/A) = 0.032, P(D/B) = 0.034 and P(D/C) = 0.056

Required probability =P(C/D)

=
`(P(D/C) P(C))/(P(D/A) P(a)+P(D/B) P(B)+P(D/C) P(C))`

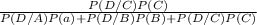
by using Bayes theorem for conditional probability

=
`(0.1*0.056)/(0.2*0.032+0.7*0.034+0.1*0.056) \\=(0.0056)/(0.0064+0.0238+0.0056) \\\\=0.156425`

32) 7 digit phone numbers with repitition including 0 will be

=
`10^7`

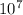
Numbers which have atleast one 7 = total number - numbers which do not have a single 7

=
`10^7 -9^7`

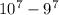
the probability that a 7-digit phone number contains at least one 7

=
`(10^7-9^7)/(10^7)`