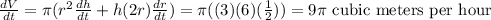Question

The surface area of a cylinder is increasing at a rate of 9 pi square meters per hour. The height of the cylinder is fixed at 3 meters. At a certain instant, the surface area is 36 pi square meters. What is the rate of change of the volume of the cylinder at that instant (in cubic meters per hour)?

Answer 1

`9\pi \text{ cubic meters per hour}`

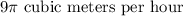
Explanation:

Since, the surface area of a cylinder,

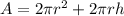`A= 2\pi r^2 + 2\pi rh` ................(1)

Where,

r = radius,

h = height,

If
`A= 36\pi\text{ square meters}, h = 3\text{ meters}`

`36\pi = 2\pi r^2 + 2\pi r(3)`

`18 = r^2 + 3r`

`\implies r^2 + 3r - 18=0`

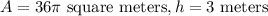
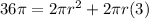
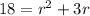
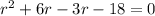`r^2 + 6r - 3r - 18 = 0` ( by middle term splitting )

`r(r+6)-3(r+6)=0`

`(r-3)(r+6)=0`

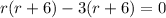
By zero product property,

r = 3 or r = - 6 ( not possible )

Thus, radius, r = 3 meters,

Now, differentiating equation (1) with respect to t ( time ),

`(dA)/(dt)= 4\pi r(dr)/(dt) +2\pi(r(dh)/(dt) + h(dr)/(dt))`

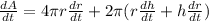
∵ h = constant, ⇒ dh/dt = 0,

`(dA)/(dt) = 4\pi r (dr)/(dt) +2\pi h (dr)/(dt)`

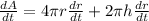
We have,
`(dA)/(dt)=9\pi\text{ square meters per hour}, r = h = 3\text{ meters}`

`9\pi = 4\pi (3) (dr)/(dt)+2\pi (3)(dr)/(dt)`

`9\pi = (12\pi + 6\pi )(dr)/(dt)`

`9\pi = 18\pi (dr)/(dt)`

`\implies (dr)/(dt) =(1)/(2)\text{ meter per hour}`

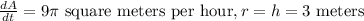
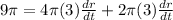
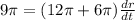
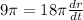
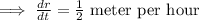
Now,

Volume of a cylinder,

`V=\pi r^2 h`

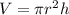
Differentiating w. r. t. t,

`(dV)/(dt)=\pi ( r^2 (dh)/(dt)+h(2r)(dr)/(dt))=\pi ((3)(6) ((1)/(2))) = 9\pi \text{ cubic meters per hour}`