Question

Use the value of the first integral I to evaluate the two given integrals. I = integral^3_0 (x^3 - 4x)dx = 9/4 A. integral^3_0 (8x - 2x^3)dx B. integral^0_3 (4x - x^3)dx C. integral^3_0 (8x - 2x^3)dx =

Answer 1

A) -9/2

B) 9/4

C) -9/2, same as A)

Explanation:

We are given that
`I=\int_0^3 x^3-4x dx=9/4`. We use the properties of integrals to write the new integrals in terms of I.

A)
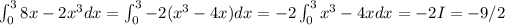`\int_0^3 8x-2x^3 dx=\int_0^3 -2(x^3-4x) dx=-2\int_0^3 x^3-4x dx=-2I=-9/2`. We have used that ∫cf dx=c∫f dx.

B)
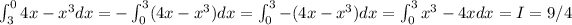`\int_3^0 4x - x^3 dx=-\int_0^3 (4x-x^3) dx=\int_0^3-(4x-x^3) dx=\int_0^3 x^3-4x dx=I=9/4`. Here we used that reversing the limits of integration changes the sign of the integral.

C) It's the same integral in A)