Answer:
W= -28.37 KJ
Step-by-step explanation:
Given
Gas is diatomic
We know that specific heat capacity ratio for diatomic gas ,γ = 1.4
P₁ = 1.4 atm ,V₁= 0.7 m³
P₂= 2.1 atm
Lets take final volume = V₂
We know that for adiabatic process
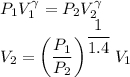

V₂ = 0.52 m³
The work done W
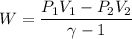
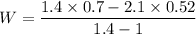
W= -0.28 atm.m³
This indicates that work is done on the gas.
W= - 0.28 atm.m³
1 atm = 101325 Pa
W= -28371 Pa.m³
W= -28.37 KJ