Question

An n × n matrix B has characteristic polynomial p(λ) = −λ(λ − 3) 3 (λ − 2) 2 (λ + 1). Which of the following statements is false? (a) rank B = 6. (b) det (B) = 0. (c) det (B TB) = 0. (d) B is invertible. (e) n = 7

Answer 1

Only d) is false.

Explanation:

Let
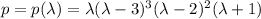`p=p(\lambda)=\lambda(\lambda-3)^3 (\lambda-2)^2 (\lambda+1)` be the characteristic polynomial of B.

a) We use the rank-nullity theorem. First, note that 0 is an eigenvalue of algebraic multiplicity 1. The null space of B is equal to the eigenspace generated by 0. The dimension of this space is the geometric multiplicity of 0, which can't exceed the algebraic multiplicity. Then Nul(B)≤1. It can't happen that Nul(B)=0, because eigenspaces have positive dimension, therfore Nul(B)=1 and by the rank-nullity theorem, rank(B)=7-nul(B)=6 (B has size 7, see part e)

b) Remember that
`p(\lambda)=\det(B-\lambda I)`. 0 is a root of p, so we have that
`p(0)=\det(B-0 I)=\det B=0`.

c) The matrix T must be a nxn matrix so that the product BTB is well defined. Therefore det(T) is defined and by part c) we have that det(BTB)=det(B)det(T)det(B)=0.

d) det(B)=0 by part c) so B is not invertible.

e) The degree of the characteristic polynomial p is equal to the size of the matrix B. Summing the multiplicities of each root, p has degree 7, therefore the size of B is n=7.