Question

If u (x) = negative 2 x^2 and v (x) = 1/x, what is the range of (uOv)(x)?

A. ( 1/3, 0 )
B. ( 3, infinite )
C. ( -infinite, 3 )
D. ( -infinite, infinite)

Answer 1

The Answer is C (-∞,3).

Explanation:

Answer 2

None of the options presented is the correct answer

Explanation:

Composite Function

Given two functions u(x) and v(x), we call the composite function
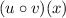`(u\circ v)(x)` to the expression u(v(x)) and
`(v\circ u)(x)`=v(u(x)).

We are given

`u(x)=-2x^2`

`\displaystyle v(x)=(1)/(x)`

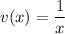
LEt's compute the composite function

`\displaystyle u(v(x))=-2((1)/(x))^2`

`\displaystyle u(v(x))=-(2)/(x^2)`

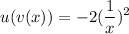
This function doesn't exist for x=0. For any other value of x, the denominator is always positive, and the function is always negative. When x tends to infinite (positive or negative), the function tends to zero. So the range of the composite function
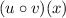`(u\circ v)(x)` is
`(-\infty,0)`

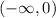
None of the options presented is the correct answer