Question

Convert from rectangular to polar coordinates:Note: Choose r and θ such that r is non-negative and 0 ≤ θ < 2πa. (6,0)b. (9,9/√3)c. (-2,2)d. (-√3,1)

Answer 1

The polar coordinates are as follow:

a. (6,2π)

b. (18, π/3)

c. (2√2 , 3π/4)

d. (2, 5π /6)

Explanation:

To convert the rectangular coordinates into polar coordinates, we need to calculate r, θ .

To calculate r, we use Pythagorean theorem:

r =
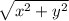`\sqrt{ x^(2) +y^(2) }` ---- (1)

To calculate the θ, first we will find out the θ ' using the inverse of cosine as it is easy to calculate.

So, θ ' = cos ⁻¹ (x/r)

If y ≥ 0 then θ = ∅

If y < 0 then θ = 2 π − ∅

For a. (6,0)

Sol:

Using the formula in equation (1). we get the value of r as:

r =
`\sqrt{6^(2) + 0^(2)  }`

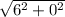
r = 6

And ∅ = cos ⁻¹ (x/r)

∅ = cos ⁻¹ (6/6)

∅ =cos ⁻¹ (1) = 2π

As If y ≥ 0 then θ = ∅

So ∅ = 2π

The polar coordinates are (6,2π)

For a. (9,9/
`√(3)`)

Sol:

r = 9 + 3(3) = 18

and ∅ = cos ⁻¹ (x/r)

∅ = cos ⁻¹ (9/18)

∅ = cos ⁻¹ (1/2) = π/3

As If y ≥ 0 then θ = ∅

then θ = π/3

The polar coordinates are (18, π/3)

For (-2,2)

Sol:

r =√( (-2)²+(2)² )

r = 2 √2

and ∅ = cos ⁻¹ (x/r)

∅ = cos ⁻¹ (-2/ 2 √2)

∅ = 3π/4

As If y ≥ 0 then θ = ∅

then θ = 3π/4

The polar coordinates are (2√2 , 3π/4)

For (-√3, 1)

Sol:

r = √ ((-√3)² + 1²)

r = 2

and ∅ = cos ⁻¹ (x/r)

∅ = cos ⁻¹ ( -√3/2)

∅ = 5π /6

As If y ≥ 0 then θ = ∅

So θ = 5π /6

The polar coordinates are (2, 5π /6)