Question

An educational organization in California is interested in estimating the mean number of minutes per day that children between the age of 6 and 18 spend watching television per day. A previous study showed that the population standard deviation was 21.5 minutes. The organization selected a random sample of n = 200 children between the age of 6 and 18 and recorded the number of minutes of TV that each person watched on a particular day. The mean time was 191.3 minutes. If the leaders of the organization wish to develop an interval estimate with 95 percent confidence, what will the margin of error be?

a) About ±2.98 minutes
b) Approximately ±1.52 minute
c) Approximately ±42.14 minutes
d) z = 1.96

Answer 1

Option A) About ±2.98 minutes

Explanation:

We are given the following information in the question:

Sample mean,
`\bar{x}` = 191.3 minutes

Sample size, n = 200

Population standard deviation, σ = 21.5 minutes

Alpha, α = 0.05

The leaders of the organization wish to develop an interval estimate with 95 percent confidence.

`z_(critical)\text{ at}~\alpha_(0.05) = \pm 1.96`

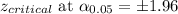
Margin of error =

`z_{\text{critical}}* \displaystyle(\sigma)/(√(n))`

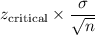
Putting the values, we get:

`\pm 1.96* \displaystyle(21.5)/(√(200)) = \pm 2.9797 \approx \pm 2.98`

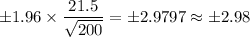
Option A) About ±2.98 minutes