Question

18) Write an equation in point-slope form for the line that is perpendicular to the given line and passes

through the given point.
y – 3 = 4(x + 2) through the point (-2,6)​

Answer 1

`\displaystyle y - 6 = -(1)/(4)(x + 2)`

Explanation:

In the Point-Slope Formula [y - y₁ = m(x - x₁)], all the negative symbols give the OPPOSITE terms of what they really are, so be EXTREMELY CAREFUL inserting the coordinates into the formula with their CORRECT SIGNS. Plus, perpendicular lines have OPPOSITE MULTIPLICATIVE INVERSE RATE OF CHANGES [SLOPES], so 4 becomes −¼.

I am joyous to assist you anytime.

Answer 2

see explanation

Explanation:

The equation of a line in point- slope form is

y - b = m(x - a)

where m is the slope and (a, b) a point on the line

y - 3 = 4(x + 2) ← is in point- slope form

with slope m = 4

Given a line with slope m then the slope of a line perpendicular to it is

`m_(perpendicular)` = -
`(1)/(m)` = -
`(1)/(4)`

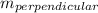and (a, b) = ( - 2, 6), then

y - 6 = -
`(1)/(4)`(x - )- 2)), that is

y - 6 = -
`(1)/(4)`(x + 2)