Question

Determine whether the function below is an even function, an odd function, both, or neither.

f(x)=(x+5)^2


A.
neither even nor odd
B.
even function
C.
both even and odd
D.
odd function

Answer 1

Option A - neither even nor odd

Explanation:

Given :
`f(x)=(x+5)^2`

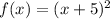
To find : Determine whether the function below is an even function, an odd function, both, or neither ?

Solution :

We know that,

1) If f(-x)=f(x) it is an even function.

2) If f(-x)=-f(x) it is a odd function.

`f(x)=(x+5)^2`

`f(x)=x^2+10x+25`

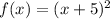
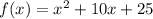
Substitute x with -x in the function,

`f(-x)=(-x+5)^2`

`f(-x)=x^2-10x+25`

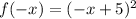
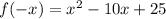
The function does not comply with the definitions.

The function is neither even nor odd.

Therefore, option A is correct.

Answer 2

A. neither even nor odd

Explanation:

The equation is that of a parabola whose line of symmetry is x=-5. Even functions are symmetrical about the line x=0, so this is not an even function. It has terms of even degree, so is not an odd function.

The function is neither even nor odd.