Question

Trevor is studying a polynomial function f(x). Three given roots of f(x) are –7, 2i, and 7. Trevor concludes that f(x) must be a polynomial with degree 3. Which statement is true?

Trevor is correct.
Trevor is not correct because –2i must also be a root.
Trevor is not correct there cannot be an odd number of roots.
Trevor is not correct because there cannot be both rational and complex roots.

Answer 1

it is option b for plato i got it right.

Explanation:

Answer 2

Option B

Trevor isn't correct because -2i must also be a root

Solution:

For the polynomial with roots -7, 2i and 7 their roots can be,

1. ) Real roots

2.) Imaginary roots

The real roots are: -7 and +7

The imaginary root given is: 2i

The imaginary roots come from the square root. So they will be in form of
`\pm 2i`

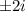
Therefore,

For f(x) with roots -7 and +7 and
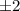`\pm 2` we have,

`f(x)=a(x+7)(x-7)(x-2i)(x+2i)`

Fundamental Theorem of Algebra states that a polynomial will have exactly as many roots as its degree (the degree is the highest exponent of the polynomial).

So for f(x) with 4 roots, degree of f(x) is 4

So option B is correct. Trevor is not correct because –2i must also be a root.