Question

(a) Find an approximation to the integral 2 (x2 − 4x) dx 0 using a Riemann sum with right endpoints and n = 8. R8 =

Answer 1

Explanation:

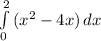`\int\limits^2_0 {(x^2-4x)} \, dx` n=8 f(x) = x² - 4x

convert [0,2] into 8 subintervals

width of each interval is

`\delta x =(2-0)/(8)=0.25`

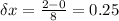
All subintervals are:

[0, 0.25], [0.25, 0.5], [0.5, 0.75], [0.75, 1], [1, 1.25], [1.25, 1.5], [1.5, 1.75] and [1.75, 2]

Let,
`x_i` be the right end point of each interval i=1,..8

`x_1=0.25, x_2=0.5, x_3=0.75, x_4=1, x_5=1.25, x_6=1.5, x_7=1.75, x_8=2`

Reiman sum is

`R_8=\delta x[f(x_1)+f(x_2)+...f(8)]\\\\0.25[f(0.25)+f(0.5)+...+f(2)]\\\\0.25*[-23.25]\\=-5.8125`