Question

10. You are given the first four terms of an arithmetic sequence. Why might you

use a recursive formula? Why might you use an explicit formula? Under what


conditions might a recursive formula be preferred over the explicit formula?


Under what conditions might an explicit formula be preferred over the


recursive formula?

Answer 1

1)It might be more convenient to write some Arithmetic Sequences as functions.

2) Whenever I need to find out any term of a given Sequence, as long as I know which value is for "n"

3)If it is known the previous term of a Sequence you might prefer it over the explicit one.

Explanation:

1) Why might you use a recursive formula?

It might be more convenient to write some Arithmetic Sequences as functions. Since you know the previous term.

Imagine we just have (...,4,... from an Arithmetic Sequence whose common difference is 5.

Example:

`\left\{\begin{matrix}f(1)=4\\f(n)=f(n-1)+5\end{matrix}\right. \Rightarrow f(2)= f(1)+5 \Rightarrow f(2)=4+5 \Rightarrow f(2)=9`

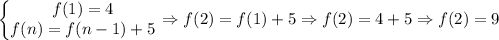
2) Why might you use an explicit formula?

Whenever I need to find out any term of a given Sequence, as long as I know which value is for "n"

For the same Sequence, let's use the explicit one:

`a_(n)=4+5(n-1) \Rightarrow a_(6)=4+5(5)\Rightarrow a_(6)=29`

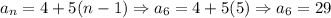
3) Under what conditions might a recursive formula be preferred over the explicit formula?

If it is known the previous term of a Sequence you might prefer it over the explicit one.