Question

Dina wants to make 15 3/4 cups of strawberry drink by mixing water and strawberry syrup with a ratio of 2 1/4 cup of water for every 3/4 cup of syrup. how much water and syrup will she need ro use?

Answer 1

The water she need is
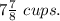`7(7)/(8) \ cups.` and strawberry syrup
`11(13)/(16)\ cups`.

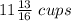Explanation:

Given:

Dina wants to make 15 3/4 cups of strawberry drink by mixing water and strawberry syrup with a ratio of 2 1/4 cup of water for every 3/4 cup of syrup.

Now, to find the quantity of water and syrup she need to use.

As given in question ratio so:

Strawberry syrup = 2 1/4 = 9/4.

Water = 3/4.

Total cups of strawberry drink = 15 3/4 = 63/4.

Let the strawberry syrup be
`(9)/(4) x`.

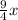And let the water be
`(3)/(4) x`.

According to question:

`(9x)/(4) + (3x)/(4)=(63)/(4)`.

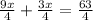On adding the fractions:

⇒
`(9x+3x)/(4) =(63)/(4)`

⇒
`(12x)/(4) =(63)/(4)`

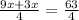
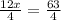
Multiplying both sides by 4 we get:

⇒
`12x=63`

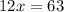
Dividing both sides by 12 we get:

⇒
`x=(63)/(12)`

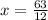
Dividing numerator and denominator by 3 on R.H.S we get:

⇒
`x=(21)/(4)`

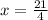
Now, putting the value of
`x` on ratios:

Strawberry syrup =
`(9)/(4)* x=(9)/(4)*(21)/(4)`

=
`(189)/(16)`

=
`11(13)/(16)\ cups`

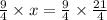
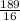
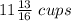
Water =
`(3)/(4)* x =(3)/(4) *(21)/(4)`

=
`(63)/(8)`

=
`7(7)/(8) \ cups.`

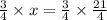
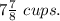
Therefore, the water she need is
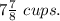`7(7)/(8) \ cups.` and strawberry syrup
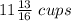`11(13)/(16)\ cups`.