Question

What are the equations of the asymptotes of the rational function?

f(x)=x^2+2x−3/2x^2−x−1

Answer 1

Vertical asymptotes :

`x=-(1)/(2) \;and\;x=1`

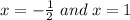
Horizontal asymptote :

`y=(1)/(2)`

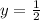
Explanation:

Consider the given rational function as,

`R(x)=(x^2+2x-3)/(2x^2-x-1) =(f(x))/(g(x))`

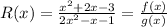
Now, to find the vertical asymptotes of the given rational function, we will first set the denominator of given rational function equal to 0 and then solve. The values at which the denominator becomes 0 gives us the vertical asyptotes of the given rational function.

Now, denominator of given rational function = g(x) = 2x²- x - 1

Now, to find vertical asymptotes, we will set g(x) = 0

∴ 2x² - x - 1 = 0

⇒2x² - 2x + x - 1 = 0

⇒2x(x - 1) + 1(x - 1) = 0

⇒(2x + 1)(x - 1) = 0

⇒2x + 1 = 0 or x - 1 = 0

`\implies\;x=-(1)/(2) \;or\;x=1`

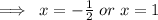
So,
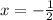`x=-(1)/(2)` and
`x=1` are the equations of vertical asymptotes of the given rational function.

In the given rational function, the degree of numerator i.e. f(x) is equal to the degree of denominator i.e. g(x), so the given rational function will have a horizontal asymptote that is given by,

`y=(coefficient\;of\;highest\;degree\;term\;in\;numerator)/(coefficient\;of \;highest\;degree\;term\;in\;denominator)`

`\implies\;y=(coefficient\;of \;x^2\;in\;numerator)/(coefficient\;of\;x^2\;in\;denominator)`

`\implies\;y=(1)/(2)`

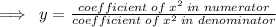
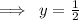
So,
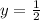`y=(1)/(2)` is the equation of horizontal asymptote of the given rational function.