Question

What is the degree of differential equation? ?​

Answer 1

Degree = 1

Explanation:

Given:

The differential equation is given as:

`(d^2y)/(dx^2)+((dy)/(dx))^2+6y=0`

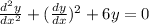
The given differential equation is of the order 2 as the derivative is done 2 times as evident from the first term of the differential equation.

The degree of a differential equation is the exponent of the term which is the order of the differential equation. The terms which represents the differential equation must satisfy the following points:

• They must be free from fractional terms.

• Shouldn't have derivatives in any fraction.

• The highest order term shouldn't be exponential, logarithmic or trigonometric function.

The above differential equation doesn't involve any of the above conditions. The exponent to which the first term is raised is 1.

Therefore, the degree of the given differential equation is 1.