Question

The Scholastic Aptitude Test (SAT) is a standardized test for college admissions in the U.S. Scores on the SAT can range from 600 to 2400.

Suppose that PrepIt! is a company that offers classes to help students prepare for the SAT exam. In their ad, PrepIt! claims to produce "statistically significant" increases in SAT scores. This claim comes from a study in which 427 PrepIt! students took the SAT before and after PrepIt! classes. These students are compared to 2,733 students who took the SAT twice, without any type of formal preparation between tries.

We also conduct a hypothesis test with this data and find that students who retake the SAT without PrepIt! also do significantly better (p-value < 0.0001). So now we want to determine if PrepIt! students improve more than students who retake the SAT without going through the PrepIt! program. In a hypothesis test, the difference in sample mean improvement ("PrepIt! gain" minus "control gain") gives a p-value of 0.004. A 90% confidence interval based on this sample difference is 3.0 to 13.0.

What can we conclude?

A. The PrepIt! claim of statistically significant differences is valid. PrepIt! classes produce improvements in SAT scores that are 3% to 13% higher than improvements seen in the comparison group.

B. Compared to the control group, the PrepIt! course produces statistically significant improvements in SAT scores. But the gains are too small to be of practical importance in college admissions.

C. We are 90% confident that between 3% and 13% of students will improve their SAT scores after taking PrepIt! This is not very impressive, as we can see by looking at the small p-value.

Answer 1

A. The PrepIt! claim of statistically significant differences is valid. PrepIt! classes produce improvements in SAT scores that are 3% to 13% higher than improvements seen in the comparison group.

False, We conduct a confidence interval associated to the difference of scores with additional preparation and without preparation. And we can't conclude that the results are related to a % of higher improvements.

B. Compared to the control group, the PrepIt! course produces statistically significant improvements in SAT scores. But the gains are too small to be of practical importance in college admissions.

Correct, since we net gain is between 3.0 and 13 with 90% of confidence and if we see tha range for the SAT exam is between 600 to 2400 and this gain is lower compared to this range of values.

C. We are 90% confident that between 3% and 13% of students will improve their SAT scores after taking PrepIt! This is not very impressive, as we can see by looking at the small p-value.

False, we not conduct a confidence interval for the difference of proportions. So we can't conclude in terms of a proportion of a percentage.

Explanation:

Notation and previous concepts

`n_1` represent the sample after the preparation

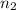`n_2` represent the sample without preparation

`\bar x_1 =678` represent the mean sample after preparation

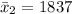`\bar x_2 =1837` represent the mean sample without preparation

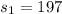`s_1 =197` represent the sample deviation after preparation

`s_2 =328` represent the sample deviation without preparation

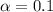`\alpha=0.1` represent the significance level

Confidence =90% or 0.90

The confidence interval for the difference of means is given by the following formula:

`(\bar X_1 -\bar X_2) \pm t_(\alpha/2)\sqrt{((s^2_1)/(n_s)+(s^2_2)/(n_s))}` (1)

The point of estimate for
`\mu_1 -\mu_2`

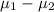
The appropiate degrees of freedom are
`df=n_1+ n_2 -2`

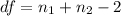
Since the Confidence is 0.90 or 90%, the value of
`\alpha=0.05` and
`\alpha/2 =0.025`, and we can use excel, a calculator or a table to find the critical value. The excel command would be: "=-T.INV(0.025,df)

The standard error is given by the following formula:

`SE=\sqrt{((s^2_1)/(n_1)+(s^2_2)/(n_2))}`

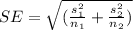
After replace in the formula for the confidence interval we got this:

`3.0 < \mu_1 -\mu_2 <13.0`

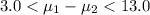
And we need to interpret this result:

A. The PrepIt! claim of statistically significant differences is valid. PrepIt! classes produce improvements in SAT scores that are 3% to 13% higher than improvements seen in the comparison group.

False, We conduct a confidence interval associated to the difference of scores with additional preparation and without preparation. And we can't conclude that the results are related to a % of higher improvements.

B. Compared to the control group, the PrepIt! course produces statistically significant improvements in SAT scores. But the gains are too small to be of practical importance in college admissions.

Correct, since we net gain is between 3.0 and 13 with 90% of confidence and if we see tha range for the SAT exam is between 600 to 2400 and this gain is lower compared to this range of values.

C. We are 90% confident that between 3% and 13% of students will improve their SAT scores after taking PrepIt! This is not very impressive, as we can see by looking at the small p-value.

False, we not conduct a confidence interval for the difference of proportions. So we can't conclude in terms of a proportion of a percentage.