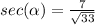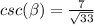Answer:
Part A)
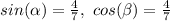
Part B)
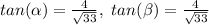
Part C)

Explanation:
Part A) Find

we know that
If two angles are complementary, then the value of sine of one angle is equal to the cosine of the other angle
In this problem
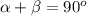 ---> by complementary angles
---> by complementary angles
so
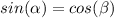
Find the value of
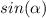 in the right triangle of the figure
in the right triangle of the figure
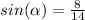 ---> opposite side divided by the hypotenuse
---> opposite side divided by the hypotenuse
simplify

therefore

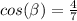
Part B) Find
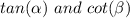
we know that
If two angles are complementary, then the value of tangent of one angle is equal to the cotangent of the other angle
In this problem
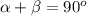 ---> by complementary angles
---> by complementary angles
so
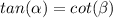
Find the value of the length side adjacent to the angle alpha
Applying the Pythagorean Theorem
Let
x ----> length side adjacent to angle alpha
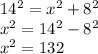
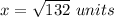
simplify

Find the value of
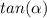 in the right triangle of the figure
in the right triangle of the figure
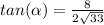 ---> opposite side divided by the adjacent side angle alpha
---> opposite side divided by the adjacent side angle alpha
simplify
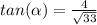
therefore
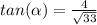
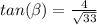
Part C) Find
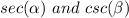
we know that
If two angles are complementary, then the value of secant of one angle is equal to the cosecant of the other angle
In this problem
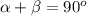 ---> by complementary angles
---> by complementary angles
so
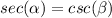
Find the value of
 in the right triangle of the figure
in the right triangle of the figure

Find the value of
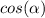
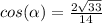 ---> adjacent side divided by the hypotenuse
---> adjacent side divided by the hypotenuse
simplify
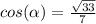
therefore