Question

The quotient property of radicals requires the indices of the radicals to be the same.

Does this mean that it is not possible to write
the ((4th root of y^3)/(square root of y)) as a single radical? Explain.

Answer 1

The radicals are the power of the same base so they can be written using rational exponents. Simplified the quotient of the exponential expression by getting a common denominator and subtracting exponents. The simplified expression is the 4th root of y

Explanation:

Got it right on edg

Answer 2

`\sqrt[4]{y}`

Explanation:

The quotient property of radicals requires the indices of the radicals to be the same.

This statement is true and is applicable also for expressing the ((4th root of y^3)/(square root of y)) as a single radical.

The given expression is

`\frac{\sqrt[4]{y^(3)}}{√(y) }`

Now,
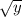`√(y)` can also be written as
`\sqrt[4]{y^(2)}`, and hence,

`\frac{\sqrt[4]{y^(3)}}{√(y) }`

=
`\frac{\sqrt[4]{y^(3)}}{\sqrt[4]{y^(2)}}`

=
`\sqrt[4]{(y^(3))/(y^(2))}`

=
`\sqrt[4]{y}` (Answer)