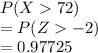Answer:
0.97725
Explanation:
Given that Professor Heinz has given the same multiple-choice final exam in his Principles of Microeconomics class for many years. After examining his records from the past 10 years, he finds that the scores have a mean of 76 and a standard deviation of 12.
i.e.
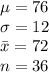
Std error of mean = sigma/sqrt n = 2
Thus the sample mean is N(76,2)
Required probability = probability that a class of 36 students will have an average greater than 72 on Professor Heinz's final exam.
=