Question

A researcher wants to estimate the true proportion of people who would buy items they know are slightly defective from thrift shops because of the lower price. After conducting a survey on a sample of 993 persons who regularly shop at thrift stores, he finds that 305 of the individuals would buy a slightly defective item if it cost less than a dollar. Calculate the lower bound of a 90% confidence interval for the true proportion of people who would purchase a defective item.

Answer 1

Answer: 0.283

Explanation:

Formula to find the lower limit of the confidence interval for population proportion is given by :-

`\hat{p}- z^*\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}`

, where
`\hat{p}` = sample proportion.

z* = Critical value

n= Sample size.

Let p be the true proportion of people who would purchase a defective item.

Given : Sample size = 993

Number of individuals would buy a slightly defective item if it cost less than a dollar = 305

Then, sample proportion of people who would purchase a defective item:

`\hat{p}=(305)/(993)\approx0.307`

Critical value for 90% confidence interval = z*=1.645 (By z-table)

The lower bound of a 90% confidence interval for the true proportion of people who would purchase a defective item will become

`0.307-(1.645)\sqrt{(0.307(1-0.307))/(993)}`

`0.307- (1.645)√(0.000214250755287)`

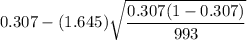
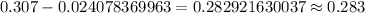`0.307- 0.024078369963=0.282921630037\approx0.283` [rounded to the nearest three decimal places.]

Hence, the lower bound of a 90% confidence interval for the true proportion of people who would purchase a defective item.= 0.283