Question

A space station in the form of a large wheel, 283 m in diameter, rotates to provide an "artif icial gravity" of 9.5 m/s 2 for people located at the outer rim. What is the frequency of the rotational motion for the wheel to produce this effect? Answer in units of rev/min.

Answer 1

The frequency of the rotational motion for the wheel to produce this effect is 2.473 rev/min.

Step-by-step explanation:

Given that,

Acceleration = 9.5 m/s²

Diameter = 283 m

We need to calculate the frequency of the rotational motion for the wheel to produce this effect

Using formula of rotational frequency

`a= r\omega^2`

`\omega=\sqrt{(a)/(r)}`

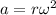
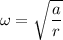
Where, r = radius

a = acceleration

`\omega` = rotational frequency

Put the value into the formula

`\omega=\sqrt{(9.5*2)/(283)}`

`\omega=0.259\ rad/s`

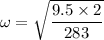
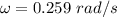
The frequency in rev/min

`\omega=0.259*(60)/(2\pi)`

`\omega=2.473\ rev/min`

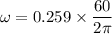
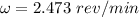
Hence, The frequency of the rotational motion for the wheel to produce this effect is 2.473 rev/min.