Answer:
Null hypothesis:

Alternative hypothesis:
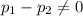
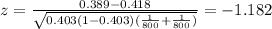

Comparing the p value with the significance level given
 we see that
we see that
 so we can conclude that we have enough evidence to FAIL to reject the null hypothesis, and we can say that we don't have significant difference between the two proportions.
so we can conclude that we have enough evidence to FAIL to reject the null hypothesis, and we can say that we don't have significant difference between the two proportions.
Explanation:
1) Data given and notation
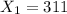 represent the number college graduates with outstanding student loans currently owe more than $50,000 (tech start-ups)
represent the number college graduates with outstanding student loans currently owe more than $50,000 (tech start-ups)
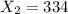 represent the number college graduates with outstanding student loans currently owe more than $50,000 ( biotech firms)
represent the number college graduates with outstanding student loans currently owe more than $50,000 ( biotech firms)
 sample 1
sample 1
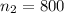 sample 2
sample 2
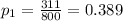 represent the proportion of college graduates with outstanding student loans currently owe more than $50,000 (tech start-ups)
represent the proportion of college graduates with outstanding student loans currently owe more than $50,000 (tech start-ups)
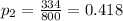 represent the proportion of college graduates with outstanding student loans currently owe more than $50,000 ( biotech firms)
represent the proportion of college graduates with outstanding student loans currently owe more than $50,000 ( biotech firms)
z would represent the statistic (variable of interest)
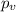 represent the value for the test (variable of interest)
represent the value for the test (variable of interest)
 significance level given
significance level given
2) Concepts and formulas to use
We need to conduct a hypothesis in order to check if is there is a difference in the two proportions, the system of hypothesis would be:
Null hypothesis:

Alternative hypothesis:
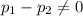
We need to apply a z test to compare proportions, and the statistic is given by:
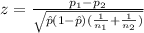 (1)
(1)
Where
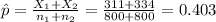
3) Calculate the statistic
Replacing in formula (1) the values obtained we got this:
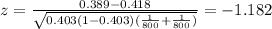
4) Statistical decision
Since is a two sided test the p value would be:

Comparing the p value with the significance level given
 we see that
we see that
 so we can conclude that we have enough evidence to FAIL to reject the null hypothesis, and we can say that we don't have significant difference between the two proportions.
so we can conclude that we have enough evidence to FAIL to reject the null hypothesis, and we can say that we don't have significant difference between the two proportions.