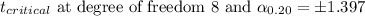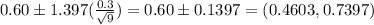Question

A sample of n = 9 college students is used to evaluate the effectiveness of a new Study Skills Workshop. Each student’s grade point average (GPA) is recorded for the semester before the workshop and for the semester after the workshop. The average GPA improved by MD = 0.60 points with s2 = 0.09. The researcher would like to use the sample to estimate how much effect the workshop would have for the entire college population. What is the 80% confidence interval for these data?​

Answer 1

80% Confidence interval: (0.4603,0.7397)

Explanation:

We are given the following in the question:

Sample mean,
`\bar{x}` = MD = 0.60 points

Sample size, n = 9

Sample variance = 0.09

Sample standard Deviation =

`=\sqrt{\text{Sample Variance}} = √(0.09) = 0.3`

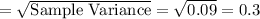
80% Confidence interval:

`\bar{x} \pm t_(critical)\displaystyle(s)/(√(n))`

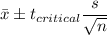
Putting the values, we get,

`t_(critical)\text{ at degree of freedom 8 and}~\alpha_(0.20) = \pm 1.397`

`0.60 \pm 1.397((0.3)/(√(9)) ) = 0.60 \pm 0.1397 = (0.4603,0.7397)`