Question

A farmer who grows genetically engineered corn is experiencing trouble with corn borers. A random check of 5,000 ears revealed the following: many of the ears contained no borers. Some ears had one borer; a few had two borers; and so on. The distribution of the number of borers per ear approximated the Poisson distribution. The farmer counted 3,500 borers in the 5,000 ears. What is the probability that an ear of corn selected at random will contain no borers?

Answer 1

The required probability is 0.4966

Explanation:

Consider the provided information.

The probability mass function of poisson distribution:
`P(X=x)=(e^(-\lambda)\lambda^x)/(x!)`

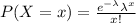
Where λ is called parameter.

It is given that The farmer counted 3,500 borers in the 5,000 ears.

Thus, the value of the parameter is:

`\lambda=(3500)/(5000)=0.7`

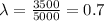
The probability that an ear of corn selected at random will contain no borers is:

`P(X=0)=(e^(-0.7)0.7^0)/(0!)`

`P(X=0)=(e^(-0.7))/(1)`

`P(X=0)\approx 0.4966`

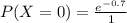
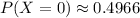
Hence, the required probability is 0.4966