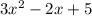Question

What is the equation, in standard form, of a parabola that models the values in the table?

Answer 1

Answer:The correct option is A).
`3x^(2) -2x+5`

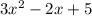
Given of x value and respective f(x) are

x f(x)

-1 10

0 5

2 13

To find f(x):

Given that f(x) is a parabola.

we know that parabola is polynomial of degree 2

The equation of parabola is ax^2+bx+c=0

For x=(-1) and f(x)=10

f(x)=
`ax^(2) +bx+c`

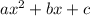
f(-1)=
`a(-1)^(2) +b(-1)+c`

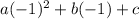
10=
`a(-1)^(2) +b(-1)+c`

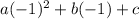
a-b+c=10 Equation 1

For x=0 and f(x)=5

f(x)=
`ax^(2) +bx+c`

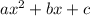
f(0)=
`a(0)^(2) +b(0)+c`

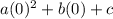
c=5 Equation 2

For x=2 and f(x)=13

f(x)=
`ax^(2) +bx+c`

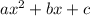
f(2)=
`a(2)^(2) +b(2)+c`

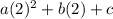
13=
`a(2)^(2) +b(2)+c`

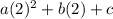
4a+2b+c=13 Equation 3

From equation 1 and equation 2,

a-b+c=10 and c=5

a-b+c=10

a-b+5=10

a-b=(5)

From equation 3 and equation 2,

4a+2b+c=13 and c=5

4a+2b+c=13

4a+2b+5=13

4a+2b=8

For value of a and b:

Equation 4: a-b=(5)

Equation 4: a-b=(5)Equation 5: 4a+2b=8

We write as,

4a+2b=8

4(5+b)+2b=8

(20+4b)+2b=8

20+6b=8

6b=-12

b=(-2)

hence,

a-b=(5)

a-(-2)=(5)

a=3

Therefore, the value of a =3, b=(-2) and c=5

Thus,

The equation of a f(x) is
`3x^(2) -2x+5`

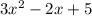
The correct option is A).
`3x^(2) -2x+5`