Question

Consider the following. {(1, −6, 3, 2), (1, 2, 0, 6)}

(a) Determine whether the set of vectors in Rn is orthogonal.
(b) If the set is orthogonal, then determine whether it is also orthonormal.
(c) Determine whether the set is a basis for Rn.

Answer 1

Answer: The required answers are

(a) NOT orthogonal.

(b) NOT orthonormal.

(c) Not a basis,

Step-by-step explanation: We are given to consider the vectors {(1, −6, 3, 2), (1, 2, 0, 6)}.

(a) We are to determine whether the set of vectors in
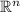`\mathbb{R}^n` is orthogonal.

(b) If the set is orthogonal, then to determine whether it is also orthonormal.

(c) To determine whether the set is a basis for
`\mathbb{R}^n`.

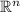We know that

any two vectors u and v are orthogonal, if their dot product u.v is zero.

The dot product of (1, −6, 3, 2) and (1, 2, 0, 6) is given by

`(1,-6,3,2).(1,2,0,6)=1*1+(-6)*2+3* 0+2*6=1-12+0+12==1\\eq 0.`

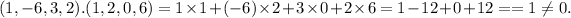
So, the given set is not orthogonal.

Since the vectors are not orthogonal, they cannot be orthonormal.

To be a basis of
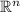`\mathbb{R}^n`, the set must contain n vectors.

Here, we are dealing with
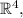`\mathbb{R}^4,` and the set contains only 2 vectors.

So, the given set cannot be a basis.