Question

Which function is divisible by (x – 3)?

A f(x) = 2x3 – 3x2 – 8x - 3
B f(x) = 2x3 + 7x2 + 2x - 3
© f(x) = 2x3 +5x2 - 4x - 3
D f(x) = 2x3 + 9x2 + 10x +3

Answer 1

a/b

Explanation:

Answer 2

From the evaluations, only option A,
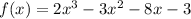`f(x) = 2x^3 - 3x^2 - 8x - 3`, gives a remainder of zero when x = 3. Therefore, option A is the function that is divisible by (x - 3).

How to determine which function is divisible by (x - 3)

To determine which function is divisible by (x - 3), use the Remainder Theorem.

According to the theorem, if a polynomial is divisible by (x - a), where 'a' is a constant, then plug 'a' into the polynomial should result in a remainder of zero.

Let's evaluate each function at x = 3 and check for a remainder of zero:

`A) f(x) = 2x^3 - 3x^2 - 8x - 3\\f(3) = 2(3)^3 - 3(3)^2 - 8(3) - 3`

= 54 - 27 - 24 - 3

= 0

`B) f(x) = 2x^3 + 7x^2 + 2x - 3\\f(3) = 2(3)^3 + 7(3)^2 + 2(3) - 3`

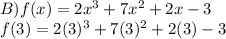
= 54 + 63 + 6 - 3

= 120 ≠ 0

`C) f(x) = 2x^3 + 5x^2 - 4x - 3\\f(3) = 2(3)^3 + 5(3)^2 - 4(3) - 3`

= 54 + 45 - 12 - 3

= 84 ≠ 0

`D) f(x) = 2x^3 + 9x^2 + 10x + 3\\f(3) = 2(3)^3 + 9(3)^2 + 10(3) + 3`

= 54 + 81 + 30 + 3

= 168 ≠ 0

From the evaluations, only option A,
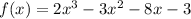`f(x) = 2x^3 - 3x^2 - 8x - 3`, gives a remainder of zero when x = 3. Therefore, option A is the function that is divisible by (x - 3).