Question

The first-order decay of radon has a half-life of 3.823 days. How many grams of radon decomposes after 5.55 days if the sample initially weighs 100.0 grams?83.4 g50.0 g36.6 g63.4 g16.6 g

Answer 1

The mass of radon that decompose = 63. 4 g

Step-by-step explanation:

R.R = P.E/(2ᵇ/ⁿ)

Where R.R = radioactive remain, P.E = parent element, b = Time, n = half life.

Where P.E = 100 g , b = 5.55 days, n = 3.823 days.

∴ R.R = 100/
`2^(5.55/3.823)`

R.R = 100/
`2^(1.45)`

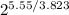
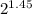
R.R = 100/2.73

R.R = 36.63 g.

The mass of radon that decompose = Initial mass of radon - Remaining mass of radon after radioactivity.

Mass of radon that decompose = 100 - 36.63

= 63.37 ≈ 63.4 g

The mass of radon that decompose = 63. 4 g