Question

What is the maximum speed at which a car can safely travel around a circular track of radius 55.0 m If the coefficient of friction between the tire and

road is 0.3502
2.60 m/s
4.39 m/s
13.7 m/s
43.0 m/s

Answer 1

13.7

Step-by-step explanation:

Took the test and got it right! <3

Answer 2

The maximum speed of the car should be 13.7 m/s

Step-by-step explanation:

For the car to travel at a maximum safe speed , the frictional force acting should be maximum and at the same time should provide the necessary centripetal force.

Let 'k' (=0.3502) be the coefficient of friction and 'N' be the normal force acting on the surface.

Then ,

N = mg , where 'm' is the mass of the body and 'g'(=9.8) is the acceleration due to gravity.

∴ Maximum frictional force , f = kN = kmg

Centripetal force that should act on the car to move with maximum possible speed is -

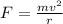`F = (mv^(2) )/(r)` , where 'v' is the velocity of the car and 'r'(=55m) is the radius of circular path.

Equating the 2 forces , we get -

`(mv^(2) )/(r) = kmg`

∴
`v = √(krg)`

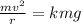
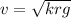
Substituting all the values , we get -

v = 13.7 m/s.