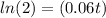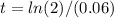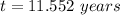Answer:
Part 1)
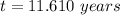
Part 2)
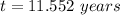
Explanation:
Part 1) we know that
The compound interest formula is equal to
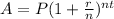
where
A is the Final Investment Value
P is the Principal amount of money to be invested
r is the rate of interest in decimal
t is Number of Time Periods
n is the number of times interest is compounded per year
in this problem we have
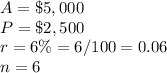
substitute in the formula above
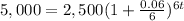
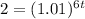
Apply log both sides
![log(2)=log[(1.01)^(6t)]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/2f85gxc3y9gt0yy6ytdyo6c8izkhve0fj4.png)
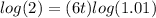
solve for t
![t=log(2)/[6log(1.01)]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/q9w5vtqcpqha3b7glznnlc1td51h01tcij.png)
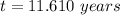
Part 2) we know that
The formula to calculate continuously compounded interest is equal to
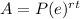
where
A is the Final Investment Value
P is the Principal amount of money to be invested
r is the rate of interest in decimal
t is Number of Time Periods
e is the mathematical constant number
we have
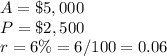
substitute in the formula above
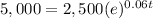
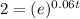
Apply ln both sides
![ln(2)=ln[(e)^(0.06t)]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/m7h6mbbvde6q0nyca4axhx2bo4lwoea5ai.png)