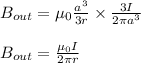A steady current I flows through a wire of radius a. The current density in the wire varies with r as J = kr, where k is a constant and r is the distance from the axis of the wi…

Question

asked Aug 1, 2020 115k views

1 Answer

Woworks · Answer 1 · 2020-08-06T11:45:48+0000

Answer:

Step-by-step explanation:

we can consider an element of radius r < a and thickness dr. and Area of this element is

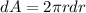
$dA=2\pi r dr$

since current density is given

J=kr

then , current through this element will be,

$di_(thru)=JdA=(kr)(2\pi\,r\,dr)=2\pi\,kr^2\,dr$

integrating on both sides between the appropriate limits,

$\int_0^Idi_(thru)=\int_0^a2\pi\,kr^2\,dr \\\\ I=(2\pi\,ka^3)/(3) -------------------------------(1)$

Magnetic field can be found by using Ampere's law

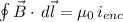
$\oint{\vec{B}\cdot\,d\vec{l}}=\mu_0\,i_(enc)$

for points inside the wire ( r<a)

now, consider a point at a distance 'r' from the center of wire. The appropriate Amperian loop is a circle of radius r.

by applying the Ampere's law, we can write

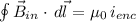
$\oint{\vec{B}_(in)\cdot\,d\vec{l}}=\mu_0\,i_(enc)$

by symmetry
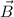$\vec{B}$ will be of uniform magnitude on this loop and it's direction will be tangential to the loop.

Hence,

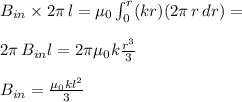
$B_(in)*2\pi\,l=\mu_0\int_0^r(kr)(2\pi\,r\,dr)= \\\\2\pi\,B_(in) l=2\pi\mu_0k (r^3)/(3) \\\\B_(in)=(\mu_0kl^2)/(3)$

now using equation 1, putting the value of k,

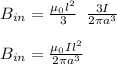
$B_(in) = (\mu_(0) l^2 )/(3 ) \,\,\, (3I)/(2 \pi a^3) \\\\B_(in) = ( \mu_(0) I l^2)/(2 \pi a^3)$

B)

now, for points outside the wire ( r>a)

consider a point at a distance 'r' from the center of wire. The appropriate Amperian loop is a circle of radius l.

applying the Ampere's law

$\oint{\vec{B}_(out)\cdot\,d\vec{l}}=\mu_0\,i_(enc)$

by symmetry
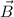$\vec{B}$ will be of uniform magnitude on this loop and it's direction will be tangential to the loop. Hence

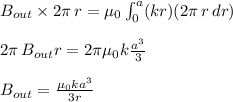
$B_(out)*2\pi\,r=\mu_0\int_0^a(kr)(2\pi\,r\,dr) \\\\2\pi\,B_(out)r=2\pi\mu_0k(a^3)/(3) \\\\B_(out)=(\mu_0ka^3)/(3r)$

again using,equaiton 1,

$B_(out)= \mu_0 (a^3)/(3r) * (3 I)/(2 \pi a^3) \\\\B_(out) = ( \mu_(0) I)/(2 \pi r)$