Question

The mean tar content of a simple random sample of 35 unfiltered cigarettes is 21.1 mg, with a standard deviation of 3.2 mg. The mean tar content of a simple random sample of 30 filtered cigarettes is 13.2 mg with a standard deviation of 3.7 mg. At a significance level of 0.01, do the results suggest that, on average, filtered cigarettes have less tar than unfiltered cigarettes?

Answer 1

There is significant evidence at 0.01 significance level that filtered cigarettes have less tar than unfiltered cigarettes

Explanation:

Let M(f) be the true mean tar content of unfiltered cigarettes

And M(u) be the true mean tar content of filtered cigarettes

Then

`H_(0)`: M(f) = M(u)

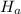`H_(a)`: M(f) < M(u)

test statistic can be calculated using the formula:

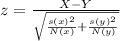`z=\frac{X-Y}{\sqrt{(s(x)^2)/(N(x))+(s(y)^2)/(N(y))}}` where

• X is the sample mean tar content of unfiltered cigarettes (21.1 mg)

• Y is the sample mean tar content of filtered cigarettes (13.2 mg)

• s(x) is the sample standard deviation of unfiltered cigarettes (3.2 mg)

• s(y) is the sample standard deviation of filtered cigarettes (3.7 mg)

• N(x) is the sample size of unfiltered cigarettes (35)

• N(y) is the sample size of filtered cigarettes (30)

Then
`z=\frac{21.1-13.2}{\sqrt{(3.2^2)/(35)+(3.7^2)/(30)}}`

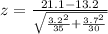
≈9.13

p-value of the statistic ≈0 <0.01 (significance level) Thus we can reject the null hypothesis.