Question

A chemist identifies compounds by identifying bright lines in their spectra. She does so by heating the compounds until they glow, sending the light through a diffraction grating, and measuring the positions of first-order spectral lines on a detector 15.0 cm behind the grating. Unfortunately, she has lost the card that gives the specifications of the grating. Fortunately, she has a known compound that she can use to calibrate the grating. She heats the known compound, which emits light at a wavelength of 461 nm, and observes a spectral line 9.95 cm from the center of the diffraction pattern.PART A:What is the wavelength emitted by compound A that have spectral line detected at position 8.55 cm?PART B:What is the wavelength emitted by compound B that have spectral line detected at position and 12.15 cm?

Answer 1

PART A: 412.98 nm

PART B: 524.92 nm

Step-by-step explanation:

The equation below can be used for a diffraction grating of nth order image:

n*λ = d*sinθ
`_(n)`

Therefore, for first order images, n = 1 and:

λ = d*sinθ
`_(1)`.

The angle θ
`_(1)` can be calculated as follow:

tan θ
`_(1)` = 9.95 cm/15.0 cm = 0.663 and

θ
`_(1)` =
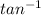`tan^(-1)` (0.663) = 33.56°

Thus: d =λ/sin θ
`_(1)` = 461/sin 33.56° = 833.97 nm

PART A:

For a position of 8.55 cm:

tan θ
`_(1)` = 8.55 cm/15.0 cm = 0.57 and

θ
`_(1)` =
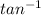`tan^(-1)` (0.57) = 29.68°

Therefore:

λ =d*sin θ
`_(1)` = 833.97*sin 29.68° = 412.98 nm

PART B:

For a position of 12.15 cm:

tan θ
`_(1)` = 12.15 cm/15.0 cm = 0.81 and

θ
`_(1)` =
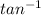`tan^(-1)` (0.81) = 39.01°

Therefore:

λ =d*sin θ
`_(1)` = 833.97*sin 39.01° = 524.92 nm