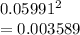Answer:
0.05991, 0.003589
Explanation:
Given that a study of the adequacy of New York City’s snow-fighting capability estimated that the number of snowstorms in a season was approximately (remember the continuity approximation) normally distributed with a mean of 6.5 and a standard deviation of 2.25.
X- number of snowstorms is N(6.5,2.25)
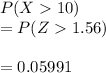
Assuming independence we can say Y the no of snowstorms >=2 is
Binomial with n =3, and p = 0.05991
the probability that New York City will have more than 10 snowstorms in at least two of the next three seasons
=