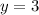Answer:
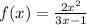
Explanation:
The function
 has a horizontal asymptote which is
has a horizontal asymptote which is
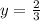
The function
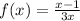 has a horizontal asymptote which is
has a horizontal asymptote which is
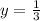
The function
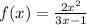 has no horizontal asymptote because the numerator has a degree which is higher than the degree of the denominator,
has no horizontal asymptote because the numerator has a degree which is higher than the degree of the denominator,
The function
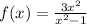 has a horizontal asymptote which is
has a horizontal asymptote which is