Question

In a photoelectric effect experiment you illuminate a metal with light of an unknown wavelength and measure the maximum kinetic energy of the photoelectrons to be 0.65 eV. Then you illuminate the same metal with light of a wavelength known to be 2/3 of the first wavelength and measure a maximum kinetic energy of 2.3 eV for the photoelectrons.

(a) Find the first wavelength, in nanometers.
(b) Find the metal's work function, in electron volts.

Answer 1

(a) 3.77 x 10^-7 m

(b) 2.65 eV

Step-by-step explanation:

According to Einstein photoelectric effect equation

`(hc)/(\lambda )-W=KE`

where, W is the work function and KE is the kinetic energy and λ be the wavelength.

(a) For first wavelength

`(6.63* 10^(-34)* 3* 10^8)/(\lambda )-W=0.65* 1.6* 10^(-19)`

`(1.989* 10^(-25))/(\lambda )-W=1.04  * 10^(-19)`... (1)

For second wavelength

λ' = 2λ/3

`(6.63* 10^(-34)* 3* 10^8* 3)/(2* \lambda )-W=2.3* 1.6* 10^(-19)`

`(2.984* 10^(-25))/(\lambda )-W=3.68  * 10^(-19)`... (2)

Subtract equation (1) from equation (2)

`(0.995*10^(-25))/(\lambda )=2.64* 10^(-19)`

λ = 3.77 x 10^-7 m

(b) Put the value of wavelength in equation (1)

`(1.989* 10^(-25))/(3.77*10^(-7) )-W=1.04  * 10^(-19)`

W = 4.24 x 10^-19 J

W = 2.65 eV

Answer 2

(a). The first wavelength is 401.0 nm.

(b). The metal's work function is 2.55 eV.

Step-by-step explanation:

Given that,

Maximum kinetic energy = 0.65 eV

Second wavelength
`\lambda_(2)= (2)/(3)*\lambda_(1)`

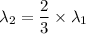
(a). We need to calculate the wavelength

Using equation of work function for first wavelength

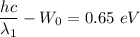`(hc)/(\lambda_(1))-W_(0)=0.65\ eV`.....(I)

For second wavelength,

`(hc)/(\lambda_(2))-W_(0)=2.3\ eV`

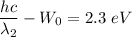
Put the value of second wavelength

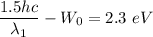`(1.5 hc)/(\lambda_(1))-W_(0)=2.3\ eV`....(II)

By subtraction equation (I) from (II)

`0.5(hc)/(\lambda_(1))=1.55`

`\lambda_(1)=(6.63*10^(-34)*3*10^(8))/(3.1*1.6*10^(-19))`

`\lambda_(1)=4.010*10^(-7)\ m`

`\lambda_(1)=401.0*10^(-9)\ m`

`\lambda_(1)=401.0\ nm`

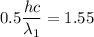
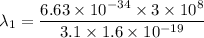
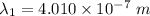
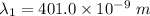
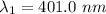
(b). We need to calculate the work function

Using formula of work function

`W_(0)=((hc)/(\lambda)-0.55)`

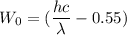
Put the value into the formula

`W_(0)=((6.63*10^(-34)*3*10^(8))/(1.6*10^(-19)*401.0*10^(-9))-0.55)`

`W_(0)=2.55\ eV`

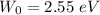
Hence, (a). The first wavelength is 401.0 nm.

(b). The metal's work function is 2.55 eV.