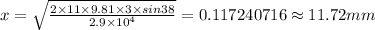Question

A block of mass 11.0 kg slides from rest down a frictionless 38.0° incline and is stopped by a strong spring with

k = 2.90 ✕ 104 N/m.
The block slides 3.00 m from the point of release to the point where it comes to rest against the spring. When the block comes to rest, how far has the spring been compressed?

Answer 1

11.72 mm

Step-by-step explanation:

The gravitational potential energy equals the potential energy of the spring hence

`PE_(gravitational)=PE_(spring)`

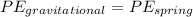
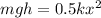`mgh=0.5kx^(2)` where m is the mass of object, g is the acceleration due to gravity, h is the height, k is the spring constant and x is the extension of the spring

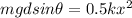`mgdsin\theta=0.5kx^(2)` where \theta is the angle of inclination and d is the sliding distance

Making x the subject then

`x=\sqrt {\frac {2mgdsin\theta}{k}}`

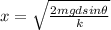
Substituting the given values then

`x=\sqrt{\frac {2* 11* 9.81* 3* sin 38}{2.9* 10^(4)}}= 0.117240716\approx 11.72 mm`