Question

$3550 $ ⁢ 3550 is invested at 10.0% 10.0 % compounded continuously. How long will it take for the balance to reach $7100 $ ⁢ 7100 ? Round your answer to two decimal places, if necessary.

Answer 1

6.93 years.

Explanation:

We have been given that $3550 is invested at 10.0% compounded continuously.

To solve our given problem, we will use continuous compounding formula.

`A=P\cdot e^(rt)`, where,

A = Final amount,

P = Principal amount,

e = Mathematical constant,

r = Interest rate in decimal form,

t = Time

`10\%=(10)/(100)=0.10`

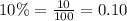
Substitute the given values:

`7100=3550\cdot e^(0.10t)`

`(7100)/(3550)=(3550\cdot e^(0.10t))/(3550)`

`2=e^(0.10t)`

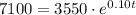
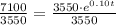
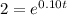
Take natural log of both sides:

`\text{ln}(2)=\text{ln}(e^(0.10t))`

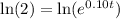
Using property
`\text{ln}(a^b)=b\cdot \text{ln}(a)`, we will get:

`\text{ln}(2)=0.10t\cdot \text{ln}(e)`

`0.6931471805599453=0.10t\cdot 1`

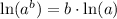`0.6931471805599453=0.10t`

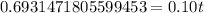
Switch sides:

`0.10t=0.6931471805599453`

`(0.10t)/(0.10)=(0.6931471805599453)/(0.10)`

`t=6.9314718`

`t\approx 6.93`

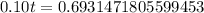
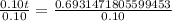
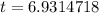
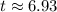
Therefore, it will take approximately 6.93 years for the balance to reach $7100.