Question

A pendulum of length L is suspended from the ceiling of an elevator. When the elevator is at rest the period of the pendulum is T. How does the period of the pendulum change when the elevator moves upward with constant acceleration?

A) The period decreases.
B) The period increases if the upward acceleration is more than g/2 but decreases if the upward acceleration is less than g/2. C) The period does not change.
D) The period becomes zero.
E) The period increases.

Answer 1

A)The period decreases.

Step-by-step explanation:

Given that

Length of the pendulum = L

Time period = T ( at rest condition)

`T=2\pi \sqrt{(L)/(g_(eff))}`

At rest condition only gravitational acceleration g act downward.

At rest
`g_(eff)=g`

`T_(at\ rest)=2\pi \sqrt{(L)/(g)}`

When acceleration will move upward with acceleration a ,then

`g_(eff)=g+a`

`T_(at\ motion)=2\pi \sqrt{(L)/(g+a)}`

Therefore we can say that time period of the pendulum will decrease ,because g+a is more than g.

Answer 2

Option A is the correct answer.

Step-by-step explanation:

When an elevator moves upward with consonant acceleration a, the overall acceleration on the body is given by

a' = a + g

So acceleration of pendulum is a + g.

We have equation for period of simple pendulum

`T=2\pi \sqrt{(l)/(a')}`

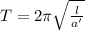
In normal case a' = g here a' is more.

From the equation we can see that period of simple pendulum is inversely proportional to square root of acceleration.

Since acceleration increases period decreases.

Option A is the correct answer.