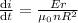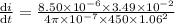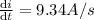Question

A long, thin solenoid has 450 turns per meter and a radius of 1.06 . The current in the solenoid is increasing at a uniform rate di/dt. The magnitude of the induced electric field at a point which is near the center of the solenoid and a distance of 3.49 from its axis is 8.50×10-6 V/m. Calculate di/dt

Answer 1

Answer:9.34 A/s

Step-by-step explanation:

Given

radius of solenoid
`R=1.06 m`

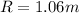
Emf induced
`E=8.50* 10^(-6) V/m`

no of turns per meter n=450

we know Induced EMF is given by

`\int Edl=-\frac{\mathrm{d} \phi}{\mathrm{d} t}=-\frac{\mathrm{d} B}{\mathrm{d} t}A`

Magnetic Field is given by

`B=\mu _0ni`

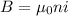
thus
`\frac{\mathrm{d} B}{\mathrm{d} t}=-\mu _0n\frac{\mathrm{d} i}{\mathrm{d} t}`

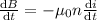
Area of cross-section

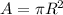`A=\pi R^2` where

solving integration we get

`E.\cdot 2\pi r=\mu _0n\frac{\mathrm{d} i}{\mathrm{d} t}\pi R^2`

where r=distance from axis

R=radius of Solenoid

`\frac{\mathrm{d} i}{\mathrm{d} t}=(Er)/(\mu _0nR^2)`

`\frac{\mathrm{d} i}{\mathrm{d} t}=(8.50* 10^(-6)* 3.49* 10^(-2))/(4\pi * 10^(-7)* 450* 1.06^2)`

`\frac{\mathrm{d} i}{\mathrm{d} t}=9.34 A/s`