Question

Ammonia gas is compressed from 21°C and 200 kPa to 1000 kPa in an adiabatic compressor with an efficiency of 0.82. Estimate the final temperature, the work required, and the entropy change of the ammonia.

Answer 1

Step-by-step explanation:

It is known that efficiency is denoted by
`\eta`.

The given data is as follows.

`\eta` = 0.82,
`T_(1)` = (21 + 273) K = 294 K

`P_(1)` = 200 kPa,
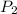`P_(2)` = 1000 kPa

Therefore, calculate the final temperature as follows.

`\eta = (T_(2) - T_(1))/(T_(2))`

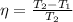
0.82 =
`(T_(2) - 294 K)/(T_(2))`

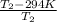
`T_(2)` = 1633 K

Final temperature in degree celsius =
`(1633 - 273)^(o)C`

=
`1360^(o)C`

Now, we will calculate the entropy as follows.

`\Delta S = nC_(v) ln (T_(2))/(T_(1)) + nR ln (P_(1))/(P_(2))`

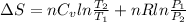
For 1 mole,
`\Delta S = C_(v) ln (T_(2))/(T_(1)) + R ln (P_(1))/(P_(2))`

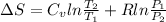
It is known that for
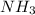`NH_(3)` the value of
`C_(v)` = 0.028 kJ/mol.

Therefore, putting the given values into the above formula as follows.

`\Delta S = C_(v) ln (T_(2))/(T_(1)) + R ln (P_(1))/(P_(2))`

=
`0.028 kJ/mol * ln (1633)/(294) + 8.314 * 10^(-3) kJ * ln (200)/(1000)`

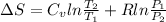
= 0.0346 kJ/mol

or, = 34.6 J/mol (as 1 kJ = 1000 J)

Therefore, entropy change of ammonia is 34.6 J/mol.