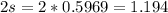Question

Suppose you fit a least squares line to 26 data points and the calculated value of SSE is 8.55. Find s^2, the estimator of sigma^2 (the variance of the random error term epsilon). What is the largest deviation that you might expect between any one of the 26 points and the least squares line? Find s^2 the estimator of sigma^2 (the variance of the random error term epsilon). S^2 (Round to four decimal places as needed.) What is the largest deviation that you might expect between any one of the 26 points and the least squares line? (Round to three decimal places as needed.)

Answer 1

The best estimator for the variance is given by:

`\sigma^2 = MSE=(SSE)/(N-2)=(8.55)/(26-2)=0.356`

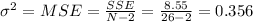
We can find the deviation taking the square root of the variance like this:

`\sigma= √(0.3563)=0.597`

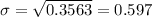
Using the empirical rule we expect to see almost all the values within two deviations from the predicted value
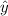`\hat y`, so then the largest deviation that you might expect would be:

`2s = 2*0.5969 =1.194`

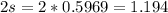
Explanation:

Analysis of variance (ANOVA) "is used to analyze the differences among group means in a sample".

The sum of squares "is the sum of the square of variation, where variation is defined as the spread between each individual value and the grand mean"

When we conduct a multiple regression we want to know about the relationship between several independent or predictor variables and a dependent or criterion variable.

If we assume that we have
`k` independent variables and we have
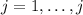`j=1,\dots,j` individuals, we can define the following formulas of variation:

`SS_(total)=\sum_(j=1)^n (y_j-\bar y)^2`

`SS_(regression)=SS_(model)=\sum_(j=1)^n (\hat y_(j)-\bar y)^2`

`SS_(error)=\sum_(j=1)^n (y_(j)-\hat y_j)^2`

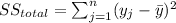
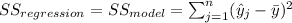
And we have this property

`SST=SS_(regression)+SS_(error)`

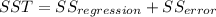
The degrees of freedom for the model on this case is given by
`df_(model)=df_(regression)=k=1` where k =21 represent the number of variables (assuming a linear model).

The degrees of freedom for the error on this case is given by
`df_(error)=N-k-1=26-1-1=24`.

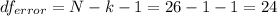Find s^2 the estimator of sigma^2 (the variance of the random error term epsilon). S^2 (Round to four decimal places as needed.)

The best estimator for the variance is given by:

`\sigma^2 = MSE=(SSE)/(N-2)=(8.55)/(26-2)=0.356`

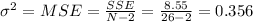
We can find the deviation taking the square root of the variance like this:

`\sigma= √(0.3563)=0.597`

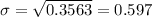
What is the largest deviation that you might expect between any one of the 26 points and the least squares line?

Using the empirical rule we expect to see almost all the values within two deviations from the predicted value
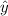`\hat y`, so then the largest deviation that you might expect would be:

`2s = 2*0.5969 =1.194`