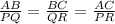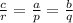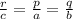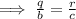Question

Triangle ABC is similar to triangle PQR, as shown below:

Two similar triangles ABC and PQR are shown. Triangle ABC has sides AB equals c, BC equals a, and AC equals b. Triangle PQR has sides PQ equals r, QR equals p, and PR equals q. Angle CAB is congruent to angle RPQ. Angle ABC is congruent to angle RQP. Angle ACB is congruent to angle QRP.


Which equation is correct?

Answer 1

`(q)/(b)=(r)/(c)`

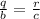
Explanation:

Consider the options for this question are as follow,

• 
  `(q)/(c)=(r)/(b)`

• 
  `(c)/(p)=(b)/(a)`

• 
  `(c)/(a)=(q)/(r)`

• 
  `(q)/(b)=(r)/(c)`

Here, In triangles ABC and PQR,

AB = c, BC = a, AC = b, PQ = r, QR = p and PR = q,

Since,

`\traingle ABC\sim \triangle PQR`

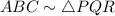
We know that,

The corresponding sides of similar triangles are in same proportion,

Thus,

`(AB)/(PQ)=(BC)/(QR)=(AC)/(PR)`

`(c)/(r)=(a)/(p)=(b)/(q)`

`(r)/(c)=(p)/(a)=(q)/(b)`

`\implies (q)/(b)=(r)/(c)`